さて、今日は「ぶったまげた!」っていうアイデア、2回目です

('20.9.12 ページ後方に追記を記述しました)
地面に図のような茶色で示す突起があったとします。まあ左からA,B,C,Dとしましょうか。
これに図の左から棒などを片持ち梁のように伸ばしてA-Dに完全に均等=同じ力をかけるにはどうしたらいいいでしょうか。
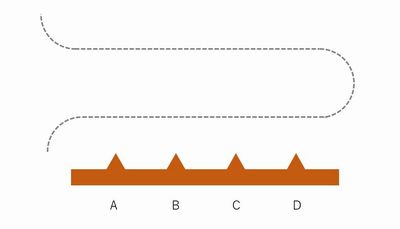
「カンタンじゃん、棒で押せばいいっしょ(゜3゜)」
はい、都合のいいお答えをありがとうございます。(^^;)
まあおっしゃる通りですが。。。
それですと棒が変形=たわむと力は不均等になっています。
接触する高さが違ってくるためです。
「じゃー無限に硬い棒で押せば良くね(゜3゜)」
はい、ありがとうございます(2回目)。
おっしゃる通りですね。それは一つの回答ではあります。
しかしこれは前回の投稿で言った
「ノーアイデア設計」「力ずく設計」「dull solution 」です。
傷ついたらゴメンなさい。
「じゃーどーすんの(゜3゜)」
はいはい。これはこう考えます。
もし仮に各点に同じ力を掛けるたなら。。
梁は逆に突起から反力として同じ力を受けます。
作用-反作用的なものですね。
(なお以下の図では突起と梁は既に接しているものとします。
説明上、離して図化します)
同値の集中荷重(≒等分布荷重)が作用した片持ち梁は。。。
二次曲線的な片持ちモーメントを受けます。
荷重を与える突起から反力として等分布荷重を受ける訳です。
そうすると。。。このように考えることができます。
通常は
(原因)梁が等分布荷重を受ける
→ (結果)二次曲線状の片持ちモーメントを受ける
これを逆にすると。。。
(原因)梁に二次曲線状の片持ちモーメントを生じさせる
→(結果)それが接する材には等分布荷重が!
おお!逆転の発想ですね! コロンブスもビックリ。
卵も立つっちゅーねん。
(上図で梁と突起は既に接しています)
このようにすると、各点には同じ力を掛けることができます。
「理屈はわかったけど具体的にどーすりゃえーの?(゜3゜)」
はいはい。それも教えますよ。
けどちょっとクレクレくんになってますよ(^^)
一つの案としては
■片持ち梁を以下のようなユニットにし
■その上下を伸縮可能な材にしておき
■これを電気制御などで押し縮みさせ
■各ユニット間でその伸び量の大きさを二次曲線的に増大させるものです。
「ちょっと複雑すぎね(゜3゜)」
あちゃ。痛いところを付かれました。あいたたた(>_<)
そのとおりですね。もっとカンタンにいかないのでしょうか。
はい、ここで先人の素晴らしい解決作をお見せします。
先程のこちら(下図)を考えると。。。
各点ごとに二次曲線状に増減する大きさのモーメント=回転力を与えるわけです。
すると。。以下のようなアイデアを考えだした人がいます。
それは。。
■荷重点位置に滑車=プーリーを設け、
■その直径を二次曲線状に増減するようにしておき、
■これに1本のヒモを掛けて、片方から引っ張る
これにより単にヒモを引っ張るだけで、同値の力を与えることができます。
おお、スゴイ。
ちょっとよくわからないかもなので別の図で言うと↓
滑車、梁、そしてそれをつなぐ軸の3つが結合している(空回りしない)状態で
滑車に掛けたひもを引っ張るとそれは回転力となり(M-P)、軸を経由して梁の回転力=曲げモーメント(M-G)として伝達されるのです。
。。で、その滑車の直径を順に二次曲線状に小さくしておくのです
その実例の模型を以下に。。。。(後続の本より)
コチラの模型では滑車は全て同径ですが、片方からのみ引っ張ることで指のように曲げる事ができます

そして下図が上記で説明した「二次曲線状に滑車径が変わる」タイプ
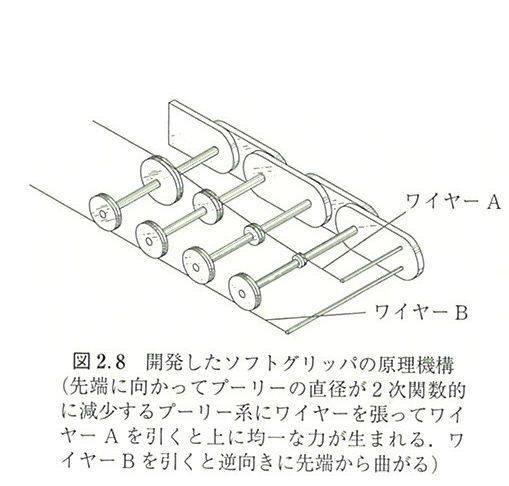
上図で内側の滑車(プーリ)が二次曲線状に径が変わっています。
外側は解除用で逆向きに回転させるもの。
上図右端は梁に相当するもの=連結ユニットで、ウロコ状に分割されています
そしてこれの実作がコチラ。その名も「ソフトグリッパー」

なんかウネウネしたちょっとキモイ感じですが、これまでのしくみより、対象物に接触するときに同じ力=等分布荷重にて接触します。
滑車はウロコのような連結ユニットに隠れて見えない状態です。
■優しく抱きしめて・/font>
f
下記はこれらをスケールアップしてなんと人を掴もうというものです

(上の把持とは「掴んで持つ」という文字通りのイミ)
同じ力=等分布荷重で接触するとは、どこも同じ力で掴むということであり、どこかだけ強く当たってイタイ、と言うことがないと言う訳です。
つまり「優しく抱きしめてくれる」ってことです・/div>
上写真で抱きしめられた美人助手も、どことなくウットリした表情になっています(当社調べ)。
今度、誰かを抱きしめる機会がありましたら等分布荷重で抱きしめてください(^^)
あ、体だけじゃなくて心も抱きしめなきゃダメですよ(^_-)ー★
いや~それにしてもよくこんなの考えついたね~

