今日はミニレクチャーです

クラシカルなコチラ。このような形式を「フィンクトラス」と言います

コチラもそう。これはmaximilian ruttiger氏による折りたたんで持ち運べる橋、というもの。




基本的な構成は左図で、全体的な応力=モーメント図は右記となります。
両端支持の単純梁(下引張)です
これも似たようなものですね(^^

これらに対し、次のような構成もあります。
これはイギリス、Royal Dockland 橋。イギリスの構造設計事務所 Technikerの設計。


次はゲーツヘッドミレニアム橋で知られるクリスウイルキンソン氏の設計のForthside橋。
空中の柱:flying strutフライイングストラットが乱れうっています(**)


いずれも床下に構造体が出ませんから、船舶、鉄道などの有効高さ=クリアランスを取るのに都合がよい形式です。
コチラのシュライヒバーガーマンのパリ、バルミーの歩道橋もそうです


これら3つは冒頭の例のものの配置を完全にひっくり返したものとなっています。
へ?ひっくり返したらケーブルは圧縮にならないの?どうなってんの(*O*)?
コレ。。実はこういうことです。上記の橋の暗示する応力(曲げモーメント)は下記です
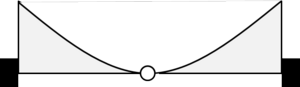
中央をピン、両端を固定とすることで上側引張となっています。2つの片持ち梁が向き合っている、と考えることも出来ます
このように(下図)考えることも出来ます。
最外端の両側の支点には引張力が働きます
Royal~橋、Forth橋とも、注意して見ると外端は引き下げのケーブルがあることが分かります。
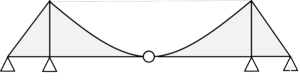
ひっくり返しても成立するとは、なかなか奥深い形式です。日本ではほとんど見たことがありません。便宜上、逆フィンクトラスと名付けしましょう
ところで、これを模式的に表すと以下となります
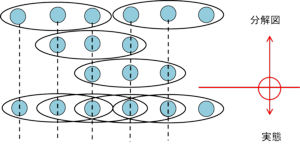
ちょっとゴチャゴチャしててわかりづらいですが。。最下段が全体の実態。残りの上段はそれの分解図です。
上段の楕円形のユニットを考え、これが両端、中央の3点で次々に隣の部材と繋がれます。図のタテ黒点線は結合点を共有していることを表します。
ひとつの結合点(ピン)は3つの部材を束ねていることになります。
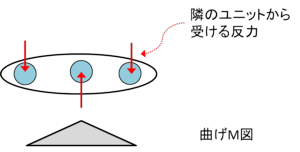
ここで1つのユニットに着目すると、3つの結合点に隣接の部材から反力を受けます。これにより図のような三角形状の曲げMを受けます。これをケーブルで忠実に再現したのがこれらの橋だということです


ところで上記は下記のような使い方も出来ます


上は建築好きならご存知、東京フォーラムのガラスの庇です
この庇は前述の通りの、三角形のユニットが互いにピン接合されて出来たものです。
これの特徴は、長~い部材を使わなくても、短いユニットを多数用いることで、自身の何十倍もの長さの梁になれる、ということです。
一人ひとりの力は小さくても力を合わせれば。。という人間社会のようなものとも言えます。
このようなものを合わせ梁とも言います。

下記は子供の頃に作ったであろう割り箸鉄砲ですが、これも、割り箸の端っこと真ん中を輪ゴムで縛ることで、割り箸自身よりも長い棒を作っています。全く同じです

コチラも同じようなものです↓

「タイトルはフィンクアーチだったけどアーチはいつ出て来るんだ?」
はい。お待たせしました。これまでは前段。 前座。オープニング・アクト。
ここからが本編です。
冒頭で、このようなフレームをお見せしました。フィンクトラスの基本形です
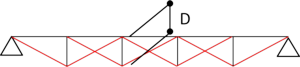
この場合、梁成Dは上図のようになります
ではこれをアーチに転用してみます。するとアラ不思議!アーチは曲がってますからこんなカンジになりました。束(短い柱)は不要です
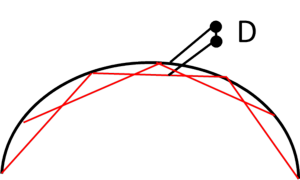
この場合でも梁成はだいたい上図のDとなります。図の赤線はケーブル(引張材)です
これを勝手にフィンクアーチと名付けます
すると以下の様な非常に都合のいいことができます。
アーチは等分布荷重などには非常に効率的に働きますが、非対称荷重などには非常に弱く、大きな曲げモーメントが生じ、それに抵抗するにはアーチを太くするなど、美的には望ましくない対処が必要となります。
ここでアーチをこのフィンクアーチにすると、フィンク材=ケーブルのおかげで成が増えたことになり、アーチの見た目(太さ)は替えずに上記の曲げモーメントに対処させることができます。
ケーブルは細くてあまり見えませんから、トラスなんかにするのよりずっと美的に望ましい結果となります
以下にテスト解析をしてみます。下図で左はフィンクアーチ、右はそれがない単なるアーチです。これに中間点に集中荷重を掛けます。
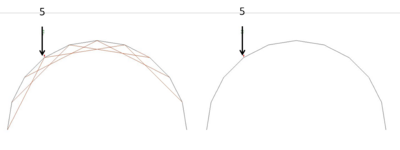
結果です。まず曲げM図では、アーチ(右)は大きな曲げモーメントを生じていますが、フィンクアーチ(左)の方は微小です
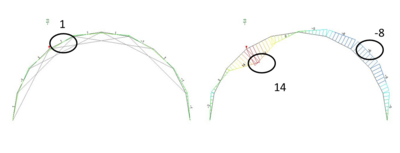
次に軸力図を見ると、フィンクアーチでは荷重点付近でアーチとケーブルに軸力が起きており、この付近で集中的に荷重を処理したことが分かります。単なるアーチの方は軸力は少なく、単なる梁として(=曲げモーメントで)対処したことが分かります
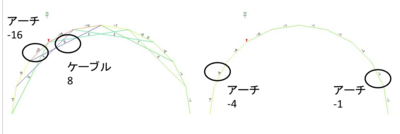
最後は変形図。まさに「ケタ違い」の結果となっています。
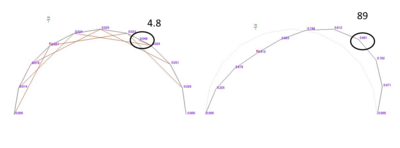
さてこの形式、別に私が発明したものではなく、既に世にあるものです。
下記は関西空港の待合室:ウイングのシェル構造。これの形状保持(ダイヤフラム)としてこの形式が用いられています。構造設計はARUP(PETER RICE)
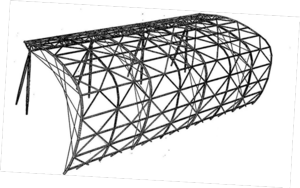
コチラはリチャード・ロジャースのテムズバレー大学の校舎。
シンプルなアーチがケーブル補強されています。コチラも構造はARUP。


ダイブ長く書きましたがいかがだったでしょうか。
「アーチが雪の偏荷重で曲げMが出て。。ええいトラスにしたれ(><)」
なんてこととはもうおサラバ。
「フィンクアーチ」。。。使ってみてください♪






コメントを残す